
Time for another Genuary, the artificially generated month of creating daily generative algorithmic art. I will post the daily images on my Mastodon, and will archive them here periodically through the month.
Today's prompt is "One color, one shape". I chose to make a hepta of heptagons made from blue heptagons.

For Genuary 2, I focused on just one of the twelve principles of animation - arcs. I've been exploring SVG <animation> elements, so I used one to animate a ball along an arc <path>. Then got carried away and made perhaps a few too many.
For Genuary 3, I'm recycling an orbit-trap fractal I shared back on Fibonacci Day (11/23, of course). It uses the typical fractal equation z ↦ zⁿ + z₀, but n increases following the Fibonacci sequence with each iteration.

I made a Julia set fractal with resolution animated starting at 6x6 pixels, increasing to 180x180 and back.
Today's prompt is to write "Genuary" without using a font. I'm always intrigued by those "Inhabited Initials" found in older books, where the first letter of a paragraph is drawn using fancy illustrations, so I attempted to write the word by pulling images of these initials from Wikimedia Commons. Initially, I wanted to automate scraping of the images from the site, but the search results were too inconsistent (searching for "A" returns images of other letters too), so I ended up manually curating the images. Try making your own words here.

For "Lights On/Off", I took a fractal image and lightened it for the lights on state, and darkened for the lights off state. Most of my fractals end up with darker backgrounds, so using a light theme was an interesting challenge.


This image simulates a set of stacked logic gates, with gate type and signal state represented by colors.

This is a (very slight) extension of last year's Genuary20 (Architecture) prompt, which I based on the skyline in the old QBasic Gorillas game. This year, it gets extended to "3D" with layers of buildings, scaled and "misted" toward the back. And stars in the sky. Give me enough genuaries, and maybe I'll eventually call this one finished...

I'm combining a cellular automaton with the concept of "odious numbers" I learned about during Mathober. Each cell is assigned one of 4 states, and if sum of states of 8 surrounding cells is an odious number, increment the state. Otherwise go back to 0.
Here is a stylized plot of r = 4 + ⌈θ/4 + 2cos(3.3θ)⌉.

A Quine is code that outputs itself. Very similar to my interpretation of last year's Genuary 3 "42 Lines of Code", this code outputs itself into a stylized image using SVG curves and gradients.
This is probably an unexpected interpretation of "Boxes Only", but I like how it turned out. Thinking of different uses of the term "box" in mathematical contexts, somehow I recalled the Box-Muller transformation, named after George E. P. Box and Mervin Muller, used to convert uniformly-distributed random numbers into a normal distribution. This is a visualization of the Box-Muller transform (which includes some rectangular boxes in there for good measure).
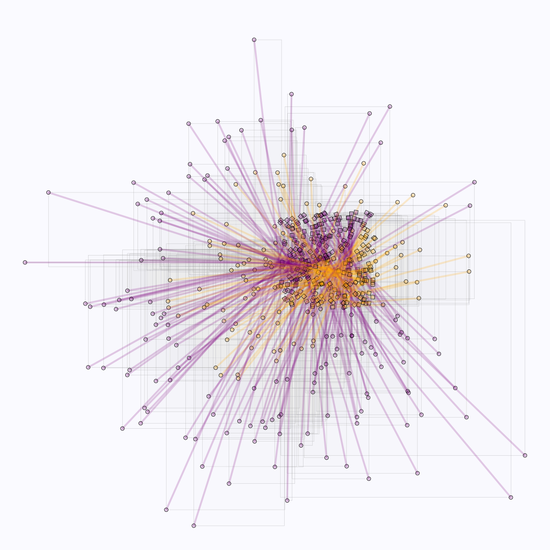
My Genuary self portrait is defined entirely by parametric equations! Portrait in the first image, equations in the second. The equations were generated by tracing points from a photograph, then basically using an FFT algorithm to convert the coordinates into paremetric equations. Each feature (head, hair, eyes, etc.) is defined by a different path.


Today's prompt seemed perfect for a Truchet tiling image, where the curve perfectly fills the space.

My "Invisible Object" animation is an experiment using SVG filters and animation effects.
Many fractals exhibit macro-scale order with micro-scale disorder, perfect for #genuary16 "Order and Disorder". The top layer is the most ordered, with entropy increasing as you go down.

This pattern uses Wallpaper Group pmg (22*), with tiles containing arbitrary bezier curves.

The prompt is "unexpected path" that follows a very simple rule. My "simple" rule returns to the concept of "odious numbers": if ⌈x⋅y⌉ is odious, turn 60 degrees counterclockwise. Otherwise, turn 60 degrees clockwise. Here, three paths with different initial points are traced for 1000 iterations of this rule.
A 16-by-16 grid of points is iterated through the mandelbrot equation and the paths of the points traced with smooth curves.

This artwork is made of a single line fractal.

The challenge was to create a poster in the style of Bauhaus. I attempted to reuse typical Bauhaus color theme and shapes, applying texture with SVG filters.

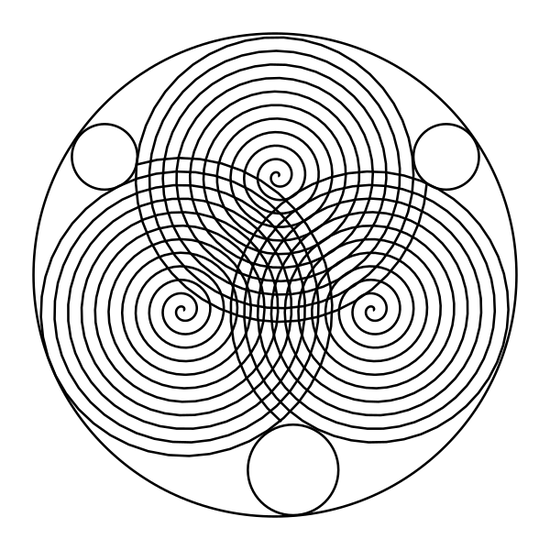
I've often been tempted to get a pen plotter, but haven't quite taken the plunge. For Genuary 22 I did some experiments with overlapping Archimedean spirals. I find them interesting since their radius is non-constant, so lining up the tangent circles becomes challenging. I still need to explore the Browne and van Wamelen paper on spiral packing - here they were just placed by brute-force.
Applying a transparency channel to a otherwise typical orbit trap fractal leads to some interesting effects. Might need to explore this one more later.

I explored several ideas for this one, where a regular grid has just a bit of randomness to make it slightly "off". The result reminds me of the tiles in my bathroom.

My favorite fractals are the ones that appear organic, like this one that reminds me of a growing vine.
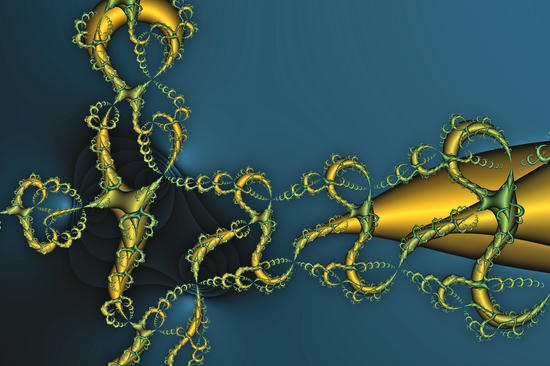
I went with a pretty minimalist pattern where each square is subdivided into 4 smaller squares.
This is another fractal with an organic look. It makes me think of some sort of plant encountered by the crew of the Enterprise in Star Trek.

This image is made entirely of HTML <div> elements, drawn using a short JavaScript that calculates a Julia Set fractal.
A screenshot of the page is shown below, with the original HTML page here.

No genetic algorithms were used in this fractal, but it always reminds me of a virus, which involves genetic mutations...

Continuing the theme of fractal images that remind me of things - this one of course looks like a bug.
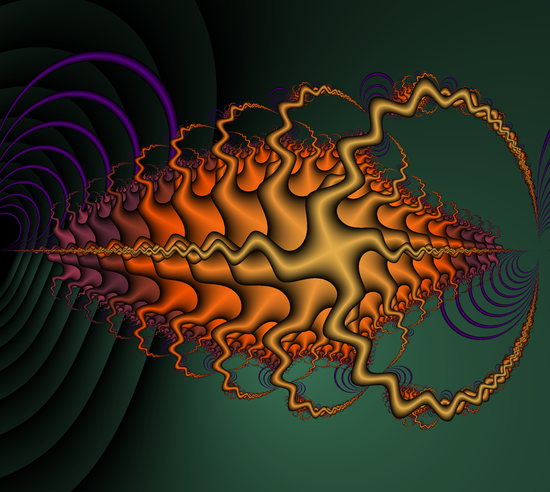
Here's a fractal animated using shaders. There is a single orbit trap along the imaginary axis, which swings left and right to make the animation. Click here for the live WebGL-rendered version.
Privacy: No cookies, no trackers, no ads.
Copyright © 2026
codeismycanvas.art