
Study art, architecture, or design for very long and you’ll run into the Golden Ratio. It is said to have aesthetically-pleasing properties, and is known to be used as long ago as ancient Rome and Greece in the design of buildings. The Golden Ratio has value φ = (1 + √5)/2, but where does that come from?
I find visualizing the ratio the easiest way to understand its value. Take a rectangle with height of 1, and width of the Golden Ratio φ. Now slice off a square from one end of the rectangle. And guess what, the little left-over rectangle has the same proportions as the original rectangle!
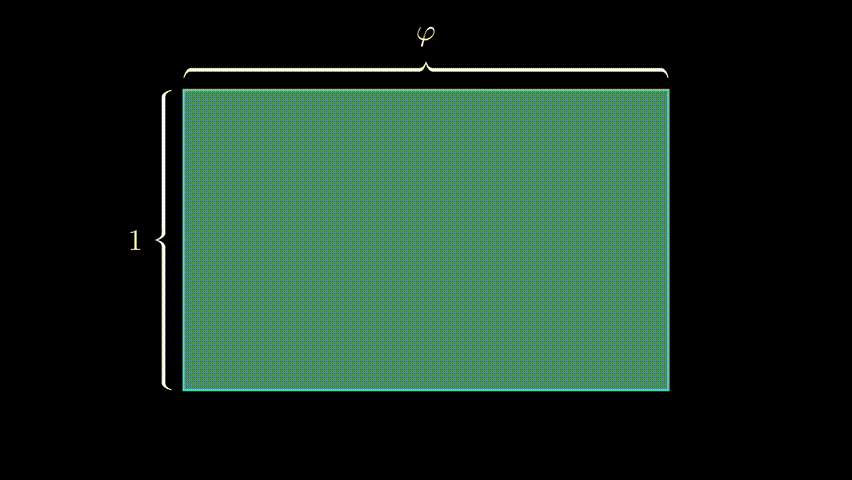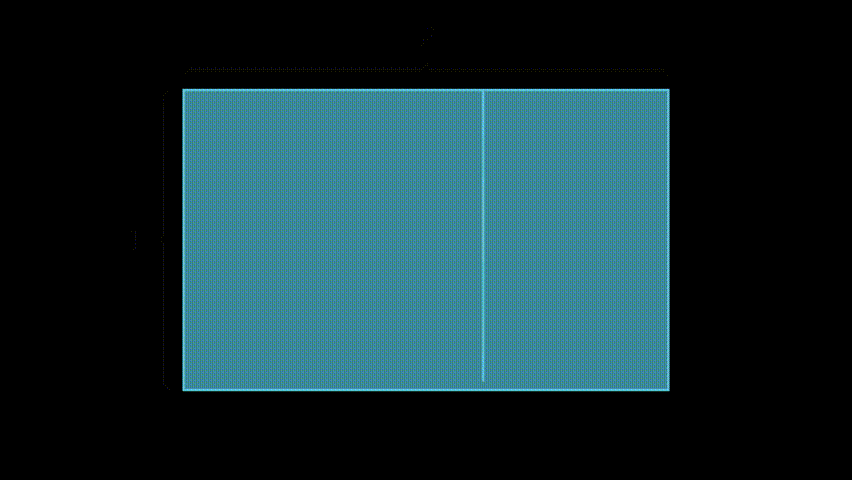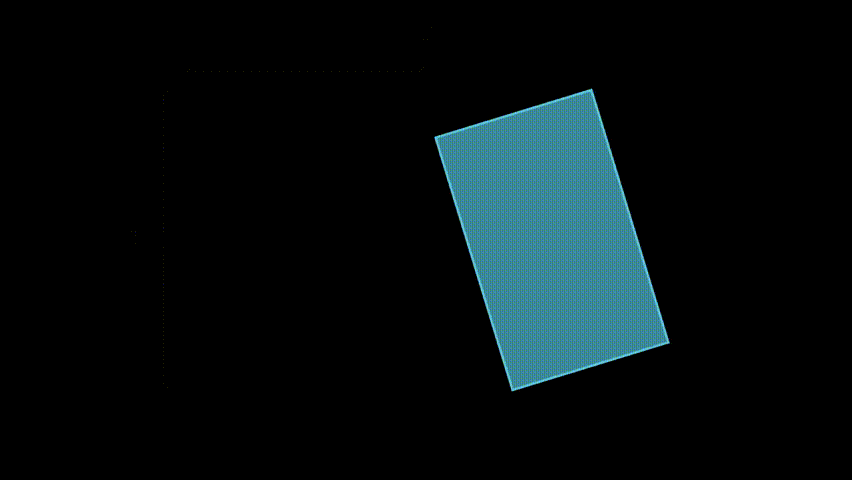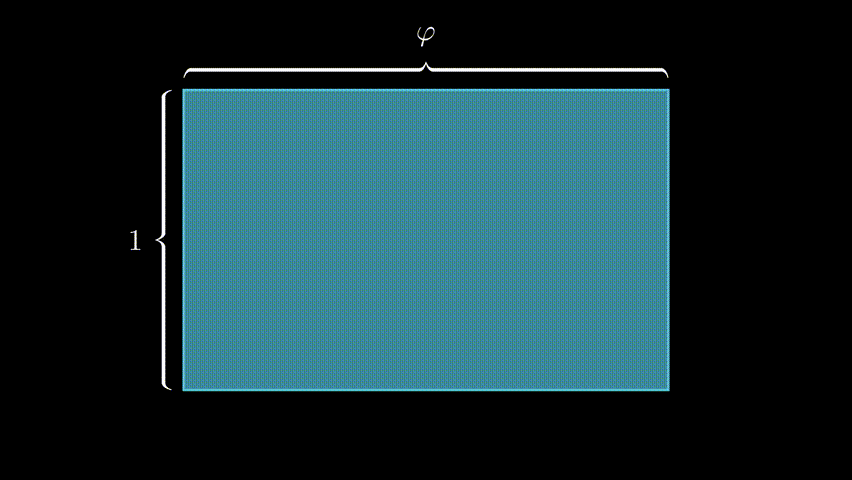
A rectangle of any other proportions wouldn’t work this way - that’s why the Golden Ratio is special, and how it’s weird value of (1 + √5)/2 is derived.
But it doesn’t need to stop there. What if we start with a longer rectangle, and slice off two squares? If the starting rectangle has just the right proportions, the bit that’s left after slicing off two squares can again be the same proportions as the original. This proportion is called the Silver Ratio, and happens to be (2 + √8)/2.

Of course we can keep going. With a rectangle using the Bronze Ratio, slice off three squares to end up with a piece the same shape and proportions as the original. The Bronze Ratio is (3 + √13)/2.

In fact, you can keep going with these “metallic ratios”. The nth ratio has a value of (n + √(n2+4))/2. Looking around the internet, I was able to find metal names for the first 10 ratios, including the Aluminum, Lead, and Tin ratios. Unfortunately, beyond the first three Olympic medal flavors, the names aren’t quite consistent across various sources.
The Golden Ratio is also famous for generating a nice logarithmic spiral. In this graphic, it is approximated using a Fibonacci sequence (in math terms, the ratio of sequential terms of the Fibonacci sequence converges on the Golden Ratio). The width of each square follows Fibonacci, and a quarter-circle is drawn across each square.

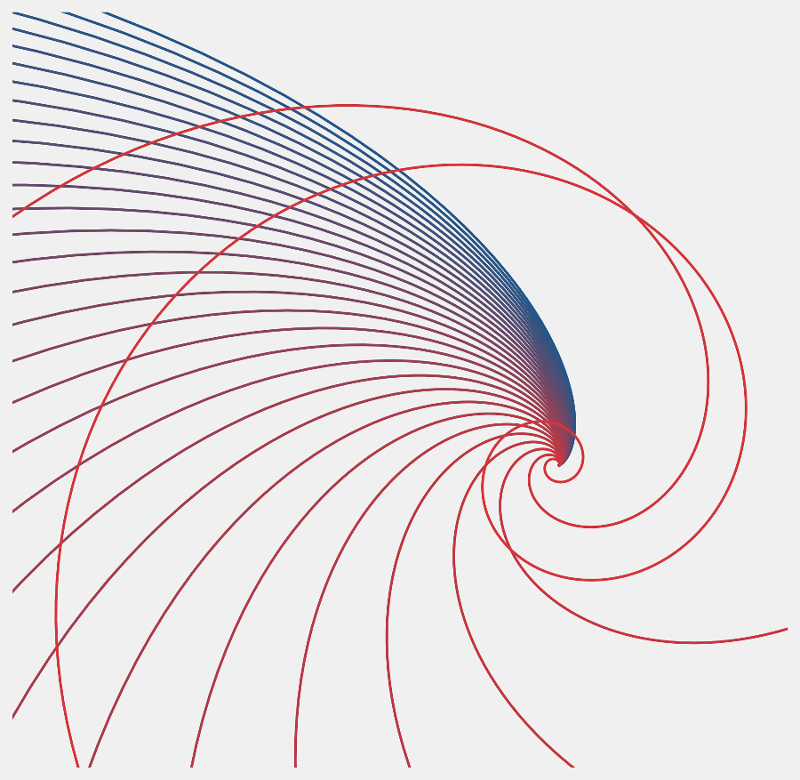
All the other metallic ratios can form spirals too. Here’s the first few, starting with the Golden Spiral in red and going out to the 30th ratio in blue (should we call it the Zinc Ratio, since zinc is the 30th element?)
Dress it up with some nice colors and a bit of texture (see Chapter 5 of my Mathematical Artwork in Python book), and turn it into math-art!

Copyright © 2025 codeismycanvas.art